
Sage: x, y = var ( 'x, y' ) sage: solve (, x, y ) ] sage: solve (, x, y ), ,, ,, ] sage: solve (, x, y ), ] sage: solutions = solve (, x, y, solution_dict = True ) sage: for solution in solutions : print ( " ". Another choice is ‘giac’.ĭomain - string (default: ‘complex’) setting this to ‘real’Ĭhanges the way SymPy solves single equations inequalities Note that SymPy is always usedįor diophantine equations. Some solutions of trigonometric equations are lost).Īlgorithm - string (default: ‘maxima’) to use SymPy’s To ‘force’ (string) omits Maxima’s solve command (useful when This keyword is incompatible with multiplicities=TrueĪnd is not used when solving inequalities. Solutions, but possibly encounter approximate solutions. Maxima’s to_poly_solver package to search for more possible To_poly_solve - bool (default: False) or string use Incompatible with to_poly_solve=True and does not makeĮxplicit_solutions - bool (default: False) require thatĪll roots be explicit rather than implicit. Multiplicities - bool (default: False) if True, There are a few optional keywords if you are trying to solve a singleĮquation.

Return a list containing one dictionary with that solution. Likewise, if there’s only a single solution, If thereĪre no solutions, return an empty list (rather than a list containingĪn empty dictionary). Return a list of dictionaries containing the solutions. Solution_dict - bool (default: False) if True or non-zero, Inequalities and systemsį - equation or system of equations (given by a

solve ( f, * args, ** kwds ) ¶Īlgebraically solve an equation or system of equations (over theĬomplex numbers) for given variables. William Stein (): added arithmetic with symbolic equations

The unit concludes with a two-day, teacher-designed project.Sage: var ( 'x y' ) (x, y) sage: f = x + 3 = y - 2 sage: f x + 3 = y - 2 sage: g = f - 3 g x = y - 5 sage: h = x ^ 3 + sqrt ( 2 ) = x * y * sin ( x ) sage: h x^3 + sqrt(2) = x*y*sin(x) sage: h - sqrt ( 2 ) x^3 = x*y*sin(x) - sqrt(2) sage: h + f x^3 + x + sqrt(2) + 3 = x*y*sin(x) + y - 2 sage: f = x + 3 < y - 2 sage: g = 2 < x + 10 sage: f - g x + 1 < -x + y - 12 sage: f + g x + 5 < x + y + 8 sage: f * ( - 1 ) -x - 3 < -y + 2īobby Moretti: initial version (based on a trick that Robert Students need to be precise in their calculations and choose efficient methods of solving as well as contextualize and decontextualize situations that can be modeled with a system of equations or inequalities. Topic C combines learning from topics A and B to explore and model with systems of equations and inequalities. Students are expected to use tools of checking solutions strategically as well as attending to precision in notation and graphing. Topic B expands students’ understanding of a single-variable inequality to linear inequalities. Students build on conceptual work from eighth grade on independence and dependence to define, create, and model with inverse functions.
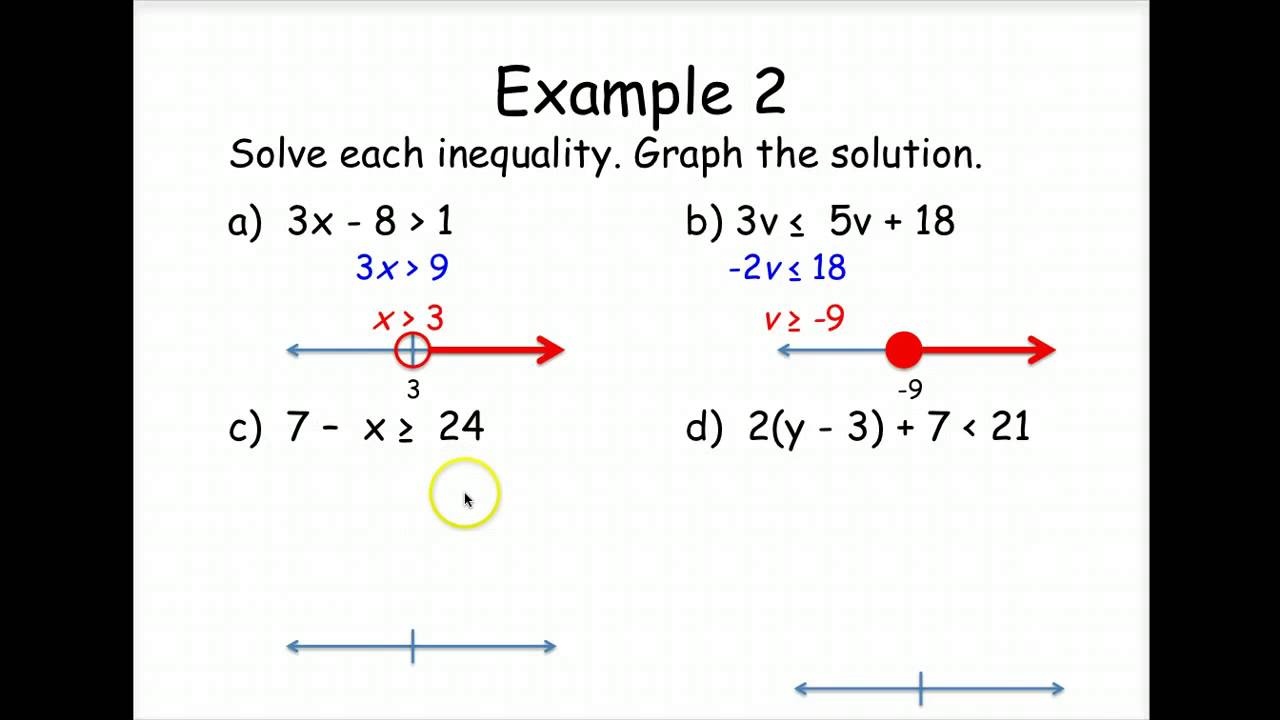
Topic A builds on work from Unit 3 to expand the idea of a solution to a coordinate point and to review identifying features of linear functions as well as graphing and writing equations in different forms to reveal properties. Proficiency of algebraic manipulation and solving, graphing skills, and identification of features of functions are essential groundwork to build future concepts studied in Units 5, 6, 7, and 8. Students are introduced to inverse functions and formalize their understanding on linear systems of equations and inequalities to model and analyze contextual situations. In Unit 4, Linear Equations, Inequalities, and Systems, students become proficient at manipulating, identifying features, graphing, and modeling with two-variable linear equations and inequalities.


 0 kommentar(er)
0 kommentar(er)
